Python Random Number Then Not Used Again

Where does python get its random numbers from?

A unproblematic explanation of modern pseudo-random number generators (PRNGs) and their new NumPy implementation

Whilst generating a sample of Ordinarily distributed numbers I was curious about where they 'came from' — especially how a estimator can create numbers that follow a distribution of choice whether that's Normal, Exponential or something more funky. Whatever method underlies creating these Normally distributed values (inversion sampling, Box-Muller or the speedy Ziggurat algorithm) they all beginning with one central building block: a sequence of uniformly distributed values.

Which then begs the question: where practice these come from? In most cases: from a 'pseudo-random number generator' — or PRNG. Having noticed that NumPy changed their default PRNG back in Jul 2019 in response to this NEP (despite the internet yet littered with the old mode to do information technology) I was bully to understand:

why they changed it
how do PRNGs work in the kickoff identify

and so write downward my thoughts in manifestly English with some helpful charts and code examples along the way. This is these notes, heavily guided past this (pretty attainable) paper and this associated lecture past Melissa O'Neill — the author of the PCG family unit of PRNGs back in 2014 that now form the default PRNG in NumPy.

Why 'pseudo'?

Because generating true randomness is hard — both for humans (endeavor your luck hither and see how you lot fare) and besides machines. If we think of machines as just taking input and producing output according to what instructions we requite them then past definition the output will be equally random as the input.

In that location are means to make sure this input is 'truly' random that generally involve hardware to measure truly random things from nature (like atmospheric noise), simply ordinarily we 'seed' algorithms with a chosen (non-random) initial value. Fifty-fifty if we use the car fourth dimension (as an integer) when the generator kicks off as the seed, this is not 100% random. However we should probably question if it is worth pursuing true randomness in the first place.

Do we want 'true randomness'?

It depends on the context. If we think about randomness as the changed of predictability, and predictability as the enemy of security, and then it can be easier to answer this question. When we are using random numbers to generate keys used for security i.due east. cryptography, then we want these numbers to seem as random equally possible to minimise the possibility of a threat. So in this case a true random number generator is useful.

In other cases when it comes to generating simulations we might have other priorities that offset against the desire for absolute zero predictability. Nosotros might be happy with a function that whilst completely deterministic and predictable when you know the starting value (or enough of the sequence), seems random when you:

don't know the starting value
knowing 'enough' of the sequence is impossible in exercise

Which then begs the next question:

What properties of PRNGs are desirable?

Speed, size and reproducibility

Naught that special here — we desire something that can generate a reproducible large quantity of random numbers fast and without taking upwardly besides much memory, particularly if we plan on having many of them running in various threads.

Uniformity

If we know that the random numbers generated will fall in the interval [0, northward] then we'd like each number in that interval to have an equal chance of existence chosen - otherwise even though theoretically we have a lot of numbers to be chosen in practise this will exist much smaller. Equally an example if we have possible numbers in the interval [0, 255] but in practise our PRNG selects simply three or 250 and then it'southward not very random at all. On the other side of things we don't necessarily want an algorithm that guarantees uniformity. If this were the case so if we accept a range of n numbers to chose from and we have already chosen north-1 numbers, then the terminal number is non random at all - information technology will merely exist the number that hasn't been selected nonetheless. Past working backwards nosotros can see that any algorithm that guarantees uniformity will diminish in randomness as nosotros achieve the end of the range - likewise known as 'period'.

A long 'flow'

If nosotros accept that in order to get a calculator to generate a sequence we have to give it a function that converts the previous number into the next number, then if we ever end upwards with a number nosotros have seen before we will get-go repeating the sequence. This is guaranteed to happen at some point as long as we choose numbers from a divisional interval considering if we select numbers in [0, n] so past definition the due north+ith number must be a repeat from a number before. In other words, over a suitable size of sequence all PRNGs will duplicate and then become deterministic. To prevent this we can make the number of numbers (the 'period') before this happens much much larger than the length of the sequence of numbers we wish to sample.

Lack of pattern

Seems like an obvious one but worth adding. For example a good algorithm to satisfy all of the to a higher place properties is simply to just 'add together 1':

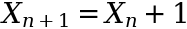
which will be:

blazingly fast, small and reproducible (nosotros just need to know X_0 the value we started with)
compatible: every number in a given interval will be chosen in one case
long period: it volition never echo as long as we never 'wrap it around' at some value to brand sure the number size doesn't get to big i.e. map a large number, y, back to zilch and get-go again

In other words the previous conditions provide the ability for a pseudo-random algorithm to appear random but do non guarantee it — nosotros still need a skillful algorithm that lacks predictability when you don't know the initial condition.

This bit is key — all PRNGs will be deterministic if you know the algorithm'south 'state' (equally in, the last random number and the function to convert that to the adjacent random number). The central is that without that info the numbers will appear random — simply like a turkey thinking that Christmas is a 'Black Swan' but the farmer non (randomness is relative to your information set).

LCGs

Linear Congruential Generators (LCGs) are one of the oldest PRNGs and fortunately pretty elementary to understand.

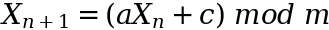
In other words — to get the next number in the sequence we take the previous number and:

multiply it by some constant a
add some other abiding c to information technology
take the residual when we separate by some other constant one thousand

So far, nothing likewise 'information science-y' with scary words or phrases like 'matrix linear recurrence' or 'Mersenne prime'. Allow'southward choose some values for {a, c, m} and run into what the output looks like.

In item let's form a generator in the fashion of a Lehmer 1951 generator which is dead uncomplicated - a=three, c=0 and in gild to ensure nosotros generate eight-chip numbers permit'due south set m=2^eight=256. This last fleck only ways that numbers will remain betwixt [0, 255] and so fit in eight-bits.

                      3, nine, 27, 81, 243, 217, 139, 161, 227, 169, 251, 241, 211, 121, 107, 65, 195, 73, 219, 145, 179, 25, 75, 225, 163, 233, 187, 49, 147, 185, 43, 129, 131, 137, 155, 209, 115, 89, eleven, 33, 99, 41, 123, 113, 83, 249, 235, 193, 67, 201, 91, 17, 51, 153, 203, 97, 35, 105, 59, 177, 19, 57, 171, 1,            3, ix, 27, 81, 243, 217, 139, 161, 227, 169, 251, 241, 211, 121, 107, 65, 195, 73, 219, 145, 179, 25, 75, 225, 163, 233, 187, 49, 147, 185, 43, 129, 131, 137, 155, 209

So what problems tin we see already?

all the numbers are odd so nosotros're not uniformly touching all numbers at all (any observable pattern being the antithesis of randomness)
the period is short — you can run across around one-half way through we get back to the get-go and then brainstorm repeating ourselves

If LCGs are and so terrible then is this relevant to PRNGs today?

Considering LCGs are not terrible. The above LCG is terrible but that is less to practice with LCGs as a family of number generators themselves and more to practise with the way we parameterised that one. In fact, the post-obit LCG is called drand48 and is what underlies java.util.Random:

but has a crucial difference with the above LCG specification.

Don't just output the 'state', but a part of information technology

In the start example we just generated the side by side number in the sequence and outputted it. If it was 255, then the adjacent number in our sequence was 255. No funny concern. In the above LCG implementation this is not the example - we have the post-obit yield seed >> 16. In python this is a bitwise operator that shifts all the bits 16 places to the right with the correct-most 16-bits getting dropped every bit a result.

We can have an example here — if nosotros have the number 1017 nosotros can stand for that in binary as 11 1111 1001 (spacing just for ease of reading) - if we do 1017 >> 3 then we end up with 111 1111 (which is 127) i.due east. we shift everything to the right by 3 places and drop the get-go 3 bits on the right. This is merely one such type of function that illustrates a way to improve our output. We now accept the following setup for our LCG algorithm:

generate the next number in the sequence — this is the 'land' of the LCG (just terminology)
apply that 'state' to generate the 'output' — this is the number that is then used to form function of the sequence

This is how we can have a 'xvi-bit generator' with an 'eight-scrap output' — because the 'country' of the generator is a xvi-fleck number just the output is an 8-bit number where that eight-bit number is created by applying some function to the 16-fleck state. As we will come across, the creation of PRNGs with a dissimilar output to land tin can drastically ameliorate their statistical properties.

Randograms: visualising randomness

In order to proceeds some intuition about how random various algorithms are we need a way to visualise this randomness. To do this nosotros'll once again borrow an idea from the paper past Melissa O'Neill. In practice random number generators are a lot bigger than what we will exercise (64-fleck country with 32-chip output) just the following is the thought:

create a generator with a state of 16-bits i.e. the seed/state is in the range[0, 65535] (where the upper bound is 2**16-ane)
output an 8-bit number that is derived from that 16-fleck state — i.eastward. every number in the output sequence will be in [0, 255]
take the sequence and group side by side points into pairs i.e. [x_0, x_1], [x_2, x_3], etc
these pairs form {x, y} co-ordinates in a 256 x 256 plot
use the PRNG to generate 2^sixteen co-ordinates and plot them where if we have no pairs for a according then that co-ordinate is white and the more pairs nosotros have on a given according the more than black that co-ordinate will be

In a manner this will requite usa a nice motion picture of randomness. If we have a good algorithm we will have a plot with lots of dots that overall looks, well, random. This will be a lot easier to see with an example. Permit's take a well parameterised "16-chip state, 8-bit output LCG" and draw out a few 'randograms'.

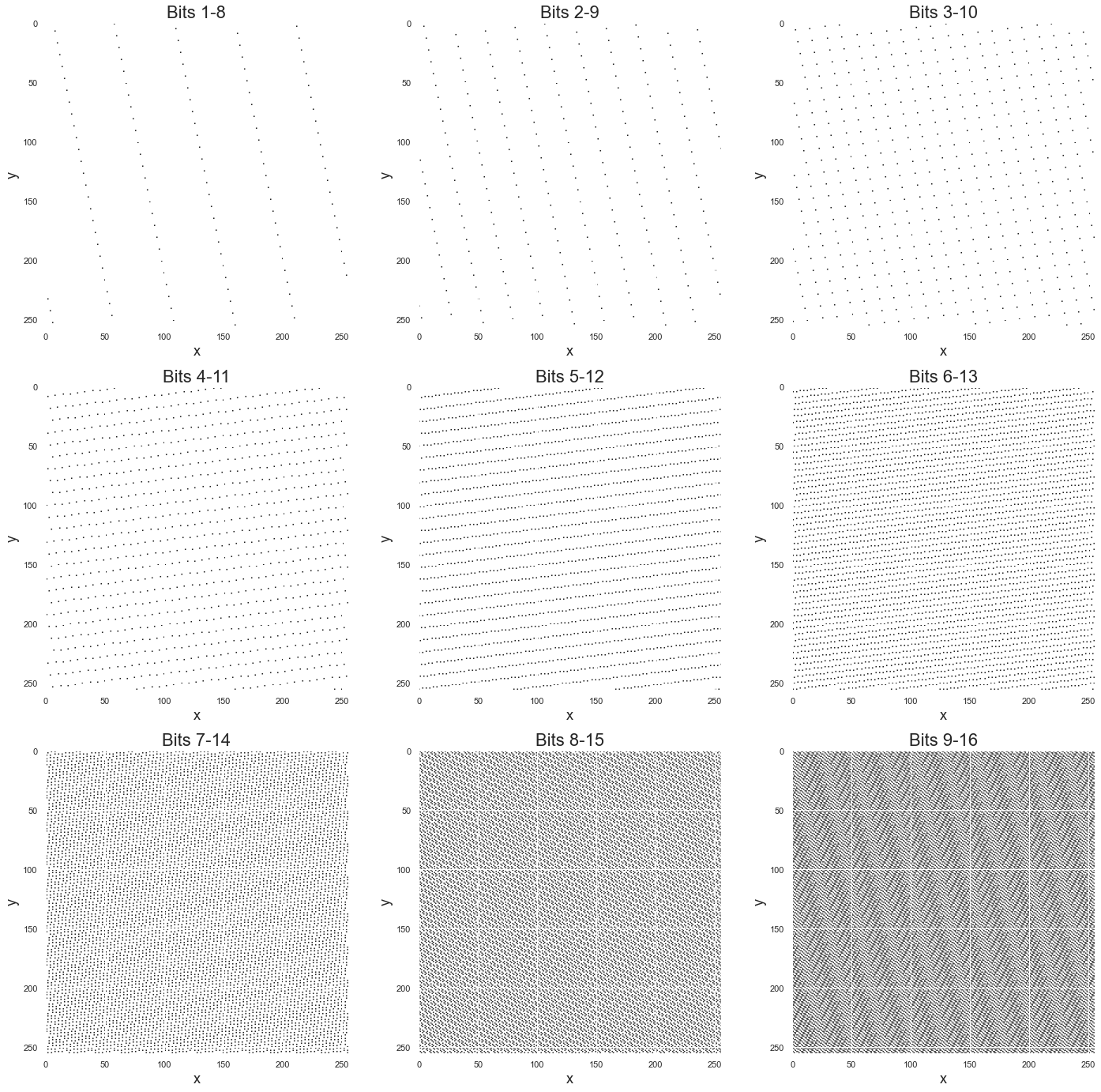
The top left nautical chart shows what nosotros get when nosotros have the right-nearly 8-$.25 of the sixteen-bit land number. For example, if our 'land' for an iteration is the number 65413 represented in binary as 1111 1111 k 0101, then we will output the right-virtually 8 bits - 1000 0101 (or 133). We practise this for all numbers, grouping them equally pairs and plot them.

Nosotros can see that the numbers don't seem very random at all — they form neat direct lines. This is Marsaglia's theorem and shows the issue with LCGs when we have too modest a period (and so get repeating values similar this). However, equally nosotros move college up the 16-flake country things commencement to await a little meliorate. There is still a clear structure in the bottom right nautical chart, merely we are doing much ameliorate in terms of roofing the space.

And so when looking at this we could make the following observation: the college the group of viii-bits in the 16-bit land number generated by a LCG, the more random they seem.

Enter PCGs

Despite LCGs nonetheless finding widespread practical apply, they were non the default PRNG for NumPy pre-2019. Instead, earlier NumPy ane.17 an algorithm chosen Mersenne Twister was used — specifically MT19937 — named because of its (absolutely jumbo) period length beingness a Mersenne Prime (two**19937 - 1 - power of two minus one). Nonetheless with the 1.17 NumPy release information technology switched over to have the default PRNG being a PCG - Permuted (Linear) Congruential Generator.

PCGs are a family of generators created past Melissa O'Neill that make clever use of the observations from the above — especially the charts. The idea is this:

outputting a function of the state, rather than the land directly, seems to increase randomness
LCGs clearly lack randomness in the lower bits (top left chart), but the higher bits tend to be 'more random' (bottom correct chart)
if we accept e.g. a 16-chip country outputting an 8-fleck number, so nosotros but need to choose eight bits to output
why don't we utilize the tiptop few bits of the xvi-fleck state, which are the most random, to choose which part nosotros apply to the remainder of the sixteen-scrap state to generate the 8-chip output
in other words, permit's apply the most random part of our state to randomly select a transform function to apply to the rest of the country — a randomised algorithm of sorts

Allow'southward have a look at a uncomplicated example.

PCG RS

The above ix charts do the following: compute an 8-bit output from a sixteen-fleck land where that 8-$.25 of output is generated by a pre-determined bit-shift (0 for the top left through to viii for the bottom right). But what almost instead of a fixed shift, a random shift?

Where do we get that randomness from? From the height few bits of our 16-scrap state. In other words, if we have a land of 57277 (1101 1111 1011 1101) we could:

utilise the elevation 2 bits, 11, to determine the shift - in this case 3
apply this shift to the other bits, 01 1111 1011 1101 due south.t. instead of selecting the left-nigh eight bits, 0111 1110, we shift forth 3 to the correct and select the bits 1111 0111

In a manner what we are doing when looking at the in a higher place 9 charts is using the randomness of the 8–15, 9–16 plots to randomly choose whether nosotros select a number from the {four-11} - {vii-14} plots. Allow'southward come across how this looks:

There's clearly still some construction there but the improvement is huge by but taking the superlative 2 bits of the 16-bit land and using this to select a permutation to the residual of the land — hence the name Permuted (Linear) Congruential Generators. But this is just one such transform — a flake shift.

What about other transforms? There are a whole host of transforms bachelor (xor, rotation etc) that create the family unit of PCGs where the top bits randomly select which permutation to use to the linearly generated land. Let'due south expect at two other such permutations that could exist used.

Rotation

One such transform that we can (randomly) select is that of a 'rotation' of the bits. Merely equally earlier with the >> operator nosotros shifted the bits to the right and dropped the overflow, with a rotation we shift one management but then instead of dropping the overflow we bring it circular the other side.

If nosotros take the number 113, represented in binary as 111 0001, we can perform a 'correct rotation' of ii to create 011 1100, or 60. Here we have taken the two correct-most $.25 (01) and rotated them around to the very start and shifted everything down.

xorshift

Some other transform we could apply is that of an 'xorshift'. Again, allow's illustrate with the same example. Again taking 113 (111 0001) we could:

'shift' it down by an corporeality e.g. ii to get 001 1100
employ the bitwise sectional or part to the original number and the shifted number

In this example we would compute xor (or ^ in python) on 111 0001 and 001 1100 to get 110 1101 (1s when only 1-bit is i, 0 if either both are 1 or 0).

PCG XSH-RS & PCG XSH-RR

At present allow'south expect at the randograms for 2 common PCGs and meet how they compare to above. They are:

PCG XSH-RS: first compute an xorshift performance, then randomly shift the resulting bits
PCG XSH-RR: first compute an xorshift operation, and so randomly rotate the resulting bits

Once again, there's still structure only they are a marked improvement. This structure exists because we are using 'minor' generators. Just as the elevation 8-bits are more random than the bottom eight-bits of a 16-fleck state, the top 16-$.25 are more than random than the bottom in a 32-bit state. Likewise as we employ a bigger and bigger state we naturally increase the period. Taking these two things together is why fifty-fifty very big (96-scrap land, 32-bit output) LCGs tin can pass Big Crush — the extensive prepare of statistical tests packaged up by Pierre L'Ecuyer and Richard Simard to examination PRNGs for the desirable properties mentioned before.

Given the added randomness of the randomly selected permutation(due south), PCGs perform much better than LCGs and as a outcome don't demand such large states to laissez passer the test suite. Information technology'south for this reason that they have been adopted as the default PRNG in NumPy — with the verbal algorithm beingness the PCG XSL RR 128/64.

gordonetione46.blogspot.com

Source: https://towardsdatascience.com/where-does-python-get-its-random-numbers-from-81dece23b712